Optipedia • SPIE Press books opened for your reference.
Jones Calculus
Excerpt from Field Guide to Polarization
The Jones matrix calculus is a matrix formulation of polarized light that consists of 2 × 1 Jones vectors to describe the field components and 2 × 2 Jones matrices to describe polarizing components. While a 2 × 2 formulation is "simpler" than the Mueller matrix formulation the Jones formulation is limited to treating only completely polarized light; it cannot describe unpolarized or partially polarized light. The Jones formulation is used when treating interference phenomena or in problems where field amplitudes must be superposed. A polarized beam propagating through a polarizing element is shown below.
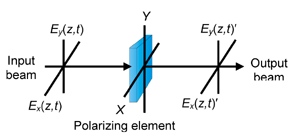
The 2 × 1 Jones column matrix or vector for the field is
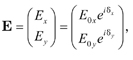
where E0x and E0y are the amplitudes, δx and δy are the phases, and i = √-1. The components Ex and Ey are complex quantities. An important operation in the Jones calculus is to determine the intensity I:
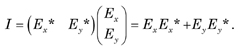
The row matrix is the complex transpose † of the column matrix, so I can be written formally as
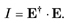
It is customary to normalize I to 1.
The Jones vectors for the degenerate polarization states are:
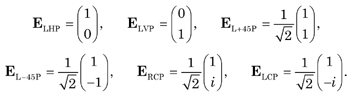
The Jones vectors are orthonormal and satisfy the relation Ei† · Ej = δij, where δij(I = j ,1, I ≠ j,0) is the Kronecker delta.
The superposition of two orthogonal Jones vectors leads to another Jones vector. For example,
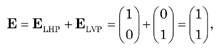
which, aside from the normalizing factor of 1/√2 , is L+45P light. Similarly, the superposition of RCP and LCP yields
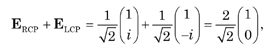
which, again, aside from the normalizing factor is seen to be LHP light. Finally, in its most general form, LHP and LVP light are
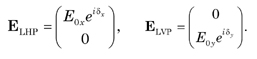
Superposing ELHP and ELVP yields
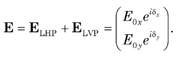
This shows that two orthogonal oscillations of arbitrary amplitude and phase can yield elliptically polarized light.
A polarizing element is represented by a 2 × 2 Jones matrix
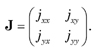
It is related to the 2 × 1 output and input Jones vectors by E' = J · E. For a linear polarizer the Jones matrix is
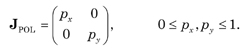
For an ideal linear horizontal and linear vertical polarizer the Jones matrices take the form, respectively,
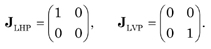
The Jones matrices for a wave plate (E0x = E0y = 1) with a phase shift of φ/2 along the x-axis (fast) and φ/2 along the y-axis (slow) are (i = √-1 )
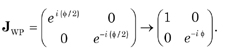
The Jones matrices for a QWP φ = π/2 and HWP φ = π are, respectively,
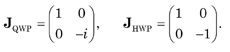
For an incident beam that is L-45P the output beam from a QWP aside from a normalizing factor is
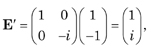
which is the Jones vector for RCP light. Finally, the Jones matrix for a rotator is
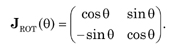
For a rotated polarizing element the Jones matrix is given by
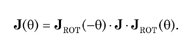
The Jones matrix for a rotated ideal LHP is
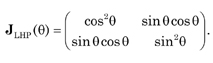
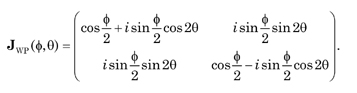
Similarly, the Jones matrix for a rotated wave plate is
For a HWP φ = π the matrix reduces to
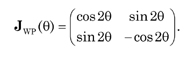
The matrix is almost identical to the matrix for a rotator except that the presence of the negative sign with cosθ rather than with sinθ along with the factor of 2 shows that the matrix is a pseudo-rotator; a rotating HWP reverses the polarization ellipse and doubles the rotation angle.
An application of the Jones matrix calculus is to determine the intensity of an output beam when a rotating polarizer is placed between two crossed polarizers.
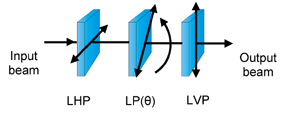
The Jones vector for the output beam is E' = J · E and the Jones matrix for the three polarizer configuration is
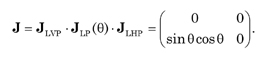
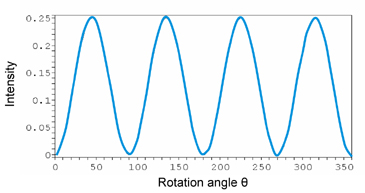
For input LHP light the intensity of the output beam is I = E'† · E' = [1 - cos(4θ)]/8.
An important optical device is an optical isolator.
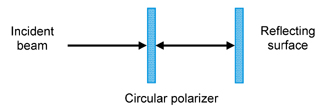
The Jones matrix equation and its expansion is
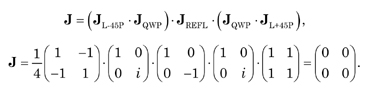
Thus, no light is returned to the optical source and the circular polarizer acts as an ideal optical isolator.
E. Collett, Field Guide to Polarization, SPIE Press, Bellingham, WA (2005).
View SPIE terms of use.

