Optipedia • SPIE Press books opened for your reference.
Axial Color
Excerpt from Optical Engineering Fundamentals, Second Edition
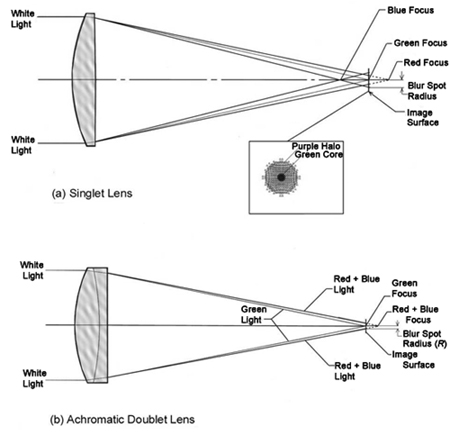
In Sec. 3.9, which dealt with dispersion, it was stated that the index of refraction for all optical glasses will vary as a function of wavelength. The index will be greater for the shorter wavelengths (blue), and the rate at which the index changes will also be greater at these shorter wavelengths. In a simple lens this results in each wavelength being focused at a different point along the optical axis. While this chromatic spreading of white light by a prism is referred to as dispersion, when it occurs in a lens, as described here, it is referred to as primary axial color. Figure 6.9(a) illustrates a simple lens focusing an axial bundle of white light. If the focus is set for the middle of the visual spectral band as shown, the blur circle will consist of a yellow-green central core with a halo of purple (red plus blue) light surrounding it. Except in very unique cases, such as laser systems or other nearly monochromatic systems, axial color is an aberration that must be dealt with in order to achieve reasonable image quality. This is most easily accomplished by converting the simple lens into an achromatic doublet as shown in Fig. 6.9(b). Here, two glass types and lens powers are selected such that the primary axial color has been corrected by bringing the two extreme wavelengths (red and blue) to a common focus. In most cases the substantial reduction in blur-circle size due to achromatization (about 10× for the visual spectrum) will result in a satisfactory design.
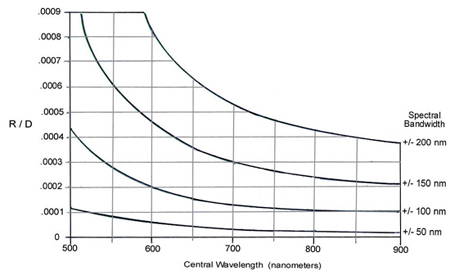
When this state of achromatization is achieved, the primary color is said to be corrected. The remaining chromatic aberration is referred to as secondary color. As Fig. 6.9(b) shows, this is due to the difference in focus between the extreme wavelengths (red and blue) and the central wavelength (green). Secondary color is often found to be the limiting axial aberration in a lens design that has otherwise been carefully designed and optimized. Because of this, it is often useful to be able to estimate the amount of secondary color that might remain after all primary aberrations have been corrected. Figure 6.10 shows a plot that makes it possible to estimate the residual blur-circle radius due to secondary color, assuming we know the diameter of the lens aperture, the central wavelength, and the spectral bandwidth that is being imaged.
When an optical system contains a series of lenses, all of which have been corrected for primary color, it is valid to add the lens diameters (based on the size of the axial light bundle) and use the sum of these diameters as the value D when using Fig. 6.10 to estimate residual secondary color. The conventional submarine periscope is an extreme example of this condition. In that case we might typically have an objective lens that is 42 mm in diameter, followed by six relay lenses, each of which is 100 mm in diameter. All of these lenses are achromatized, i.e., corrected for primary color over the visual spectral band. If we assume that spectral band to be 560, +/-50 nm, we will find from Fig. 6.10 a value for R/D that is 0.00008. Knowing the cumulative lens diameter to be 642 mm, we can then solve for the blur spot radius R = 0.00008 × 642 = 0.050 mm. The resulting resolution limit at the final image will be about cycles/mm. This periscope design will contain an eyepiece with an EFL of 71.5 mm to view the final image with a magnification of This eyepiece magnification will boost the visual resolution capability to about 25 cycles/mm. From this we can conclude that the image quality of the periscope optics is consistent with the capability of the typical viewer's eye. It has been found that, when this optical system is to be used for a high-quality photographic application, the secondary color does become a limiting factor and a color filter will be required to reduce the spectral bandwidth in order to take advantage of the film's resolution capability.
B. Walker, Optical Engineering Fundamentals, Second Edition, SPIE Press, Bellingham, WA (2008).
View SPIE terms of use.